In questi giorni la rete ed i media parlano e straparlano di un simpatico (e totalmente inconsapevole) polpo in un acquario, che, a detta di molti, avrebbe incredibili capacità divinatorie, in quanto avrebbe previsto i risultati di tutte le principali partite giocate nel Mondiale di Calcio in Sudafrica. Ovviamente, questo polpo, soprannominato "Paul", non ha alcun potere mistico, e le sue azzeccatissime previsioni sono da considerare puramente casuali. In fondo, si sa, la fortuna è cieca.
Recentemente, ho parlato di come si misura la plausibilità di un'ipotesi evolutiva. In particolare, alcuni lettori hanno chiesto se e come sia possibile distinguere ipotesi alternative più o meno robuste. Un albero lungo 3 steps più dell'ipotesi parsimoniosa è un'alternativa valida o va scartato?
Non esiste un "valore soglia" oltre il quale un'ipotesi alternativa diventa inaccettabile. Questo perché il numero degli step evolutivi non è una misura assoluta (come la temperatura in Kelvin), ma varia in funzione del numero di caratteri e di taxa presenti nella matrice. Un'indicazione più affidabile si può ottenere cambiando punto di vista. Per capirlo, ritorniamo al nostro caro polpo Paul.
Il polpo Paul si può considerare un elaboratore casuale che ha ricostruito la sequenza delle vittorie nel campionato mondiale di calcio. Dato che il sistema in analisi era relativamente semplice (poche partite, tutte con solo due possibili esisti), il nostro Paul ha prodotto per puro caso una descrizione molto affidabile del sistema. Quindi, è chiaro che anche un elaborazione casuale di dati può produrre una rappresentazione corretta della realtà. Come possiamo, quindi, stabilire se una previsione (o una ipotesi) in accordo con i dati è "vera" oppure solamente casualmente "azzeccata" (come nel caso delle previsioni di Paul)? In statistica esistono modi per misurare se e quanto un modello sia in accordo con i dati "per davvero" oppure solo "per caso". In generale, si definisce "ipotesi nulla" la condizione ottenuta "per caso". Un modello è ritenuto quindi accettabile se è possibile dimostrare statisticamente che esso NON può essere ricavabile dall'ipotesi nulla. La questione è più complessa, ma non mi voglio dilungare ed impantanare nella statistica: mi basta che abbiate compreso il concetto.
Bene... qualcuno chiederà dove siano i theropodi in questo post che cita polpi e football.
Vi ricordate le varie anime del BAND, la (ridotta) cerchia di studiosi che negano un'origine dinosauriana per gli uccelli? Una delle principali obiezioni dei sostenitori del BAND è che le numerose somiglianze anatomiche tra uccelli e dinosauri theropodi siano il prodotto di due fenomeni separati, due linee evolutive che solo per caso hanno sviluppato grande somiglianza morfologica.
Secondo il BAND, quindi, l'ipotesi che lega uccelli e theropodi sarebbe solo l'effetto della casuale evoluzione di strutture simili in taxa distanti. Proviamo ad accettare il modello BAND e ritorniamo al discorso della misurazione del caso.
Se il BAND ha ragione, allora l'ipotesi nulla è che le somiglianze tra uccelli e dinosauri sono casuali. In base a questa ipotesi, dovremmo quindi ipotizzare che un test statistico tra le varie versioni del BAND e l'ipotesi BAD (Birds Are Dinosaurs) non potrebbe trovare una differenza significativa tra questi differenti alberi. Ovvero, se potessimo dimostrare che la differenza tra gli alberi BAND e quello BAD non è distinguibile da una differenza ottenibile casualmente (ad esempio, elaborata da un super-polpo Paul incaricato di costruire alberi filogenetici), allora dovremmo ammettere che l'ipotesi che lega dinosauri e uccelli, per quanto più parsimoniosa delle altre (quelle BAND) non ha sufficiente robustezza statistica per essere proclamata "corretta".
Un metodo utilizzato per questo genere di valutazioni è il Test di Templeton, il quale misura appunto la probabilità che la differenza tra due alberi evolutivi creati dalla stessa matrice sia riconducibile all'ipotesi nulla, ovvero, sia una mera casualità statistica. Si assume che se il Test di Templeton produce una probabilità minore del 5%, allora non si può escludere l'ipotesi nulla, e, quindi, non ci sono sufficienti dati per affermare che un'ipotesi è migliore dell'altra, in quanto la loro differenza (in steps) è indistinguibile da quella ottenibile casualmente.
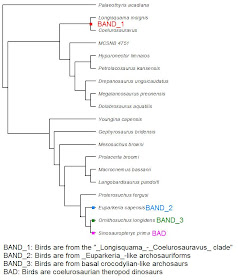
Albero di Reptilia basato sulla matrice di Senter (2004) modificata omettendo Archaeopteryx. Le posizione alternative di Archaeopteryx in base alle varie ipotesi BAND e BAD sono indicate dai quadrati colorati.
Ho quindi effettuato il Test di Templeton sulla matrice di Senter (2004), la quale contiene un uccello (Archaeopteryx), un theropode non-aviano (Sinosauropteryx), un rappresentante della linea evolutiva dei coccodrilli (Ornithosuchus), l'arcosauriforme basale Euparkeria e i bizzarri rettili Longisquama e Coelurosauravus, ovvero, è una matrice che include tutti i protagonisti delle versioni del BAND e del BAD contemporaneamente.
L'albero più parsimonioso è (ovviamente) quallo BAD, che colloca Archaeopteryx sulla linea theropode. Quanto misurerebbero le altre ipotesi, confrontate con la parsimoniosa?
L'ipotesi che collocherebbe Archaeopteryx con i coccodrilli basali (BAND_3) è 7 steps più lunga del BAD.
L'ipotesi che collocherebbe Archaeopteryx con Euparkeria (BAND_2) è 11 steps più lunga del BAD.
L'ipotesi che collocherebbe Archaeopteryx con Longisquama e Coelurosauravus (BAND_1) è 20 steps più lunga del BAD.
Già queste misure potrebbero bastare, ma, qual'è la loro significatività statistica, in base al Test di Templeton?
Il Test produce i seguenti valori di probabilità per l'ipotesi che il BAD sia migliore dei BAND solamente per caso: per l'ipotesi BAND_3 ha lo 0.8% di probabilità, per il BAND_2 ha lo 0.09% di probabilità, mentre per il BAND_1 ha lo 0.03% di probabilità. Tutti questi valori sono molto molto più bassi del 5% considerato come limite minimo di probabilità per ammettere l'ipotesi nulla, e, quindi, dimostrano che il BAD è una spiegazione migliore dei BAND, e che non si può minimamente sostenere che ciò sia dovuto solamente a fattori casuali.
Nemmeno il polpo Paul potrebbe salvare il BAND...
Bibliografia:
Senter P., 2004 - Phylogeny of Drepanosauridae (Reptilia: Diapsida). Journal of Systematic Palaeontology, 2(3): 257-268.

Vox Polypi, Vox Dei
RispondiEliminaHai per caso già scritto un articolo che elenchi o comunque spieghi le ragioni dei sostenitori della BAND? Ho provato a cercare nel blog ma non ho trovato nulla. Grazie in anticipo
RispondiEliminaSimone
Digita "B.A.N.D."
RispondiEliminaPerfetto. Grazie mille.
RispondiEliminaSimone